Overview
On this page, we introduce the basic concepts of sample space and events, and we discuss/review some basic set theory & algebra.
Important
The basic and advanced learning objectives listed below are meant to give you an idea of the material you should learn about this section. These are mainly intended to be used in a course which uses an Active Learning approach, where students are required to “read ahead” before each class - but can equally be used in a more traditional course setting.
Unless your teacher gives you specific instructions, it is up to you to decide how much of the listed resources you need to read or watch - you probably do not need to go through all of it. You might also want to look at the General Study Tips & Tricks page for some recommendations on how to effectively study with a math textbook and videos.
The first time you look at a page like this one, you will probably want to skip ahead to the “To prepare for class” section - and then come back to the rest of this page later.
Basic learning objectives
These are the tasks you should be able to perform with reasonable fluency when you arrive at your next class meeting. Important new vocabulary is indicated in italics.
-
Understand the definition of a sample space, and an event.
-
Understand the definitions and basic properties of the union, intersection, and complement operations on sets, and the basics of set algebra.
-
Determine whether two events are mutually exclusive or not.
Advanced learning objectives
In addition to mastering the basic objectives, here are the tasks you should be able to perform after class, with practice:
-
Effectively use the laws of set algebra, including DeMorgan’s law, to rewrite and simplify expressions.
-
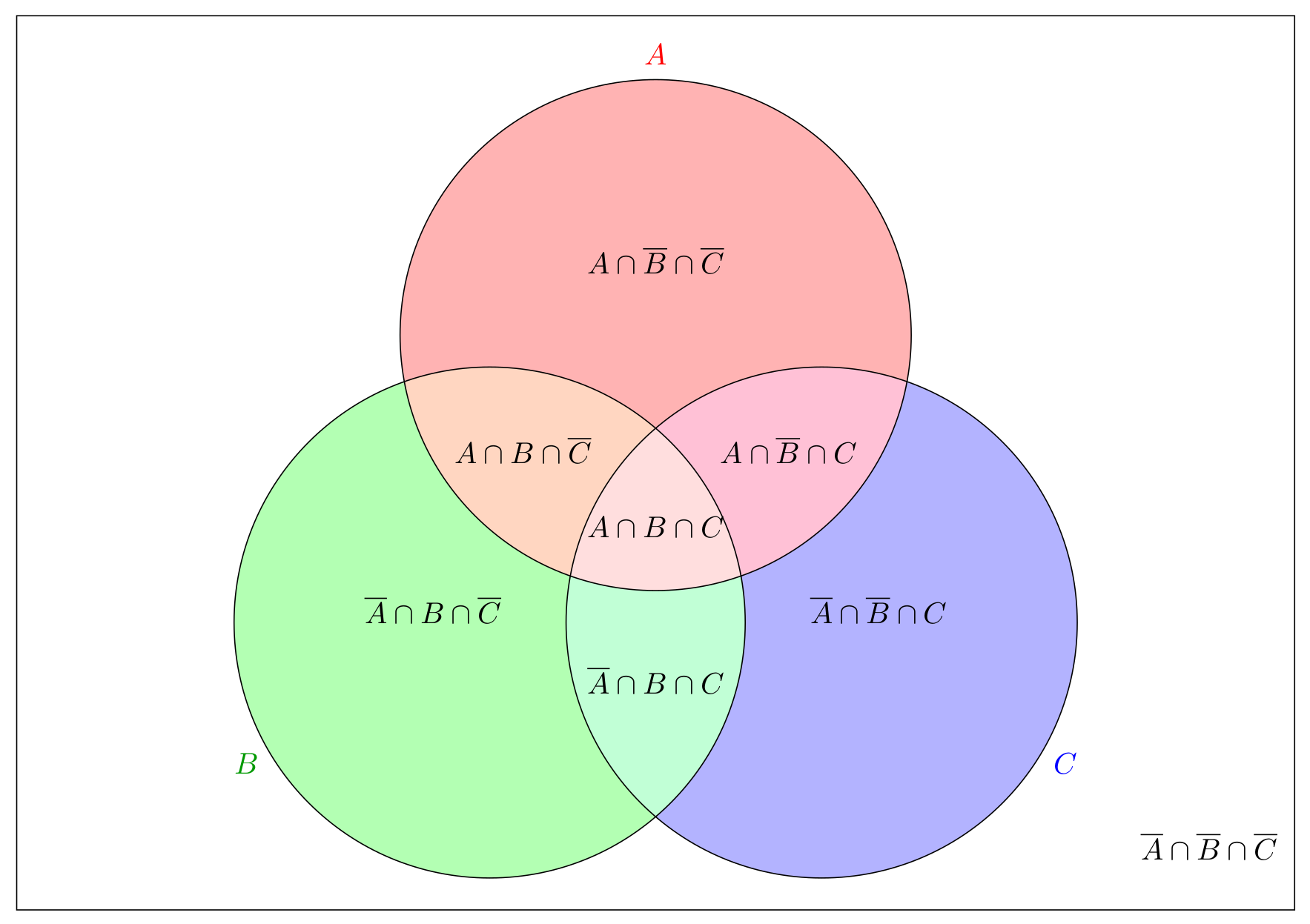
Effectively identify each region in a general Venn diagram of 3 sets, and write it as a simple intersection of 3 sets, e.g. as \(\overline{A}\cap B\cap \overline{C}\).
-
Apply the Inclusion-Exclusion Principle for 2 or 3 sets and use this to fill in all missing cardinalities in a Venn diagram of 3 sets.
-
Use appropriate notation with indexing for unions and intersections of a sequence of events.
-
Distinguish between discrete and continuous sample spaces, as well as between countably and uncountably infinite sets.
To prepare for class
-
Consider a procedure that has many possible outcomes, such as rolling a die or flipping a coin. A set of all possible outcomes for such a procedure is called a sample space, and is usually denoted with the greek letter \(\Omega\).
-
Watch the following video (by Brendan Cordy, 4m35s) showing some examples of sample spaces:
-
Any subset \(E \subseteq \Omega\) is known as an event. Events are typically denoted by capital letters taken from near the beginning of the latin alphabet.
-
Watch the following video (by Brendan Cordy, 4m11s) showing some examples of events:
-
While working with events, we will often make use of the following basic operations on sets:
- The union of two sets \(A\) and \(B\) (written \(A \cup B\)),
- the intersection (written \(A \cap B\)), and
- the complement of a set \(A\) (written either as \(A^{c}\), \(\overline{A}\), or \(A'\)).
We also need the notion of set containment: If the set \(A\) is completely contained within the set \(B\), we write \(A\subseteq B\) (where the half-equal sign symbolizes the possibility that in fact \(A\) and \(B\) are equal).
You’re probably familiar with these operations, but it’s worth reviewing the laws of set algebra. Most of these laws are evident from the definitions of the set operations, so there’s no need to commit them to memory. For example, \(A \cup B = B \cup A\) or \(((A)^c)^c = A\).
-
Watch this video (by jbstatistics, 15m16s) explaining the set operations of union, intersection, and complement in the context of probability (note that the video also already shows some examples of assigning numbers to the “probabilities” of events, which we will look at in more detail later and which you may ignore for now). The video also explains when two events are called mutually exclusive (or disjoint):
-
Watch the following video (by OnlineMathClass, 3m) which explains the Inclusion-Exclusion Principle for counting the number of elements in the union of two sets:
After class
-
While most laws of set algebra are quite straight-forward, DeMorgan’s Laws and the Distributive Laws are not as obvious, and are worth reviewing:
DeMorgan’s Laws:
- \((A \cup B)^c = A^c \cap B^c\)
- \((A \cup B)^c = A^c \cap B^c\)
Distributive Laws:
- \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)
- \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)
-
Exercise: Simplify the expression \((A^c \cap (B \cup A))^c\) by applying the laws of set algebra one at a time. (You should obtain \(A \cup B^c\).)
-
Watch this video (by jbstatistics, 7m40s) explaining DeMorgan’s Laws and how to use them to calculate certain probabilities:
-
Watch the following video (by Ms. Hearn, 7m23s) which shows how to place all elements of a given finite universal set (the sample space in the context of probability) into the appropriate regions of a Venn diagram:
-
Carefully study the following general Venn diagram of three sets, which shows how the various subsets can always be expressed as triple-intersections (note that in this image, the complement \(A^C\) of a set \(A\) is denoted with a bar, i.e. by \(\overline{A}\)):
Further ressources
-
(Optional) Watch these short videos (by Mike Black, each 3-5min) as you deem necessary to refresh your memory about sets, set notation, Venn diagrams, and the various operations we can apply to sets:
-
Watch these videos (by Numberphile, 8m, and Vsauce, 24m13s, respectively) about the difference between countably infinite and uncountably infinite sets, and some interesting paradoxes involving them: