Differentiability implies Continuity

Theorem: If a function \(f\) is differentiable at \(x = a\), then it must be continuous at \(x = a\).

Proof:

We must show that when the limit \(\lim_{h \to 0} \frac{f(a+h)-f(a)}{h}\) exists (and equals \(f'(a)\)), then the limit \(\lim_{x \to a} f(x)\) is equal to \(f(a)\). Notice that in one limit we have the variable \(h\) approaching 0 and in the other the variable \(x\) approaching \(a\). To obtain the second limit based on the first, it seems like we should first try to write the second limit also using the variable \(h\) approaching 0. If we replace \(x\) by \(a+h\) in the limit \(\lim_{x \to a} f(x)\), then \(x \to a\) becomes \(a+h \to a\) and this occurs as \(h \to 0\). Therefore,

So what we really need to show is that when the limit \(\lim_{h \to 0} \frac{f(a+h)-f(a)}{h}\) exists, then the limit \(\lim_{h \to 0} f(a+h)\) is equal to \(f(a)\). We do this by starting with \(\lim_{h \to 0} f(a+h)\) and rewriting it algebraically until we can use \(f'(a) = \lim_{h \to 0} \frac{f(a+h)-f(a)}{h}\):

Derivative of Power Functions

Theorem: For any nonzero real number, if \(f(x) = x^n\), then \(f'(x) = nx^{n-1}\).

Proof when \(n\) is a positive integer:

We have

Even though we actually don’t need to know the details of the expansion of \((x+h)^n\), you may want to read about the Binomial Theorem to understand this in more detail.

Proof when \(n\) is any nonzero real number (this requires logarithmic differentiation):

Let \(y = x^n\), then \(\ln |y| = \ln |x^n| = n \,\ln|x|\). Implicitly differentiating the equation \(\ln |y| = n\,\ln |x|\) on both sides with respect to \(x\) gives \(\frac{y'}{y} = \frac{n}{x}\) and we therefore obtain \(y' = \frac{n\,y}{x} = \frac{n\,x^n}{x} = n\,x^{n-1}\).

Derivative of Exponential Functions

Theorem: For any positive real number \(a\), if \(f(x) = a^x\), then \(f'(x) = a^x \ln(a)\).

Proof: Let us first compute the derivative of the exponential function \(g(x) = e^x\). We have

Here we have used that the number \(e\) (“Euler’s number) can in fact be defined to be the unique number which satisfies the equation \(\displaystyle \lim_{h \to 0} \frac{e^h - 1}{h} = 1\) (see Exercise 13d in section 2.1).

This gives the extremely important special case \(\boxed{\tfrac{d}{dx} e^x = e^x}\), that is evaluting \(e^x\) gives us both its function value and the slope of its tangent line.

We are now ready to consider a general exponential function, \(f(x)=a^x\) for any \(a>0\), by using the Chain Rule:

For any number \(N\), we have \(\displaystyle N = e^{\ln N}\), since the exponential function and the logarithmic function in base \(e\) are both inverse functions of each other. Replacing \(N\) by \(a^x\) gives \(\displaystyle a^x = e^{\ln a^x} = e^{x \ln a}\) where a well-known property of logarithms is used to obtain the last expression. To differentiate \(a^x\), we can therefore differentiate the equivalent expression \(\displaystyle e^{x \ln a}\) and apply the Chain Rule:

The Sum Rule

Theorem: If \(f(x)\) and \(g(x)\) are differentiable functions with derivatives \(f'(x)\) and \(g'(x)\) respectively, then \(\frac{d}{dx}[f(x) + g(x)] = f'(x) + g'(x)\).

Proof:

Note that we can break the initial limit as the sum of two limits since these limits both exist by assumption, the assumption being that both functions \(f\) and \(g\) are differentiable.

The Product Rule

Theorem: If \(f\) and \(g\) are differentiable functions, then their product \(P(x) = f(x) \cdot g(x)\) is also a differentiable function, and

Proof:

Based on the definition of the derivative, we have

and we need to show that this is actually equal to \(f(x) g'(x) + g(x) f'(x)\).

Note that the individual derivatives of \(f\) and \(g\) are

so we somehow have to make sure that these appear in our limit.

To do this, we will try to rewrite the numerator to make appear expressions such as \(f(x+h)-f(x)\) and \(g(x+h)-g(x)\). By looking at the following figure we can see how this is possible: Assume \(f(x)\) and \(g(x)\) are the two sides of a rectangle and that \(f(x+h)\) and \(g(x+h)\) are the sides of a rectangle with longer sides. In other words we assume when evaluating \(f\) and \(g\) at \(x+h\) instead of \(x\) that both function values have increased. This may not actually be the case, but it helps to visualize the expression that will replace the numerator in our limit.

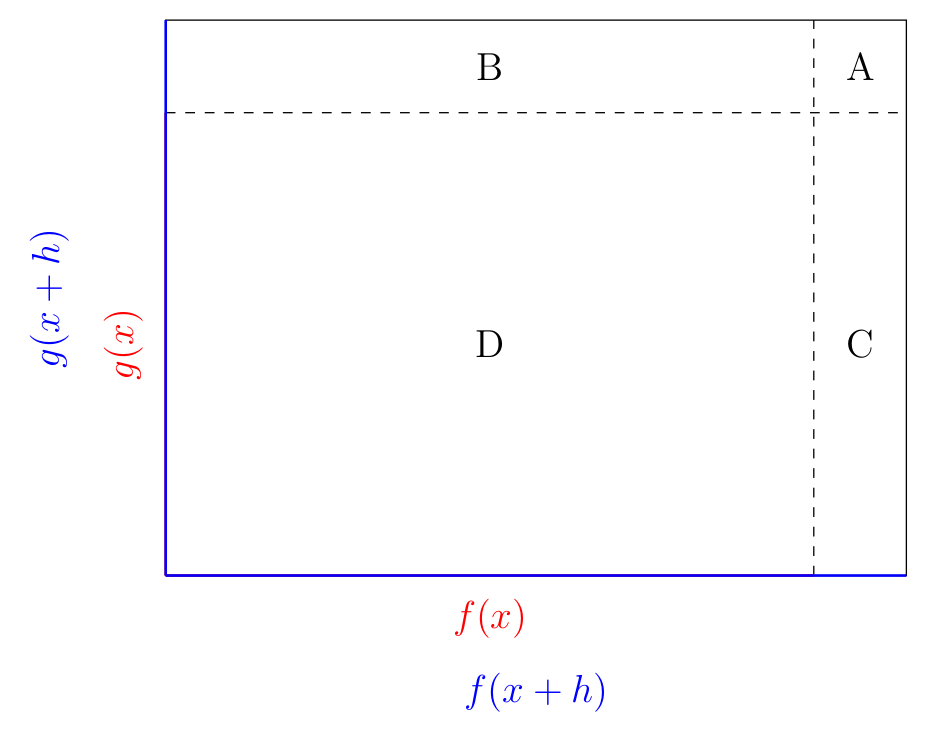
From the figure, we can see that the numerator in our limit, \(f(x+h)g(x+h) - f(x)g(x)\), corresponds to the difference of the areas of the largest rectangle (with side lengths \(f(x+h)\) and \(g(x+h)\)) and the rectangle with side lengths \(f(x)\) and \(g(x)\), i.e. to the difference \((A+B+C+D) -D\):

Therefore we can replace this numerator by the expression that represents the sum of the areas of the rectangles \(A\), \(B\), and \(C\). Since \(\color{orange}{A=[f(x+h)-f(x)][g(x+h)-g(x)]}\), \(\color{darkgreen}{B=f(x)[g(x+h)-g(x)]}\), and \(\color{purple}{C=g(x)[f(x+h)-f(x)]}\), we obtain:

Notice that we have used the fact that the limit of a sum is the sum of the limits when those limits exist, and that \(g\) is a continuous functions (can you tell where this is used and why it is true?). Furthermore, you should note that this proof is actually completely independent of the figure since expanding shows algebraically that:

Derivatives of Sine and Cosine Functions

Theorem: For all real numbers \(x\),

Proof:

The proof is largely based on a very important result concerning the sine function (it is used for example to study the motion of the pendulum in classical mechanics):

where angles are measured in radians (an angle’s measurement in radians is equal to the length of the arc spanned by the angle in a unit circle). We first start by proving this result:

Let’s start with a unit circle (radius is 1) centered at point A. Assume \(x\) is the angle (measured in radians) at A of a sector of the circle (assume for now that \(x\) is acute) and that points B and C are the other two vertices of the sector. We also draw a line going through B perpendicular to the segment AB. This line intersects in point D the line going through points A and C so that \(\triangle ABD\) is a right triangle (see the following figure):

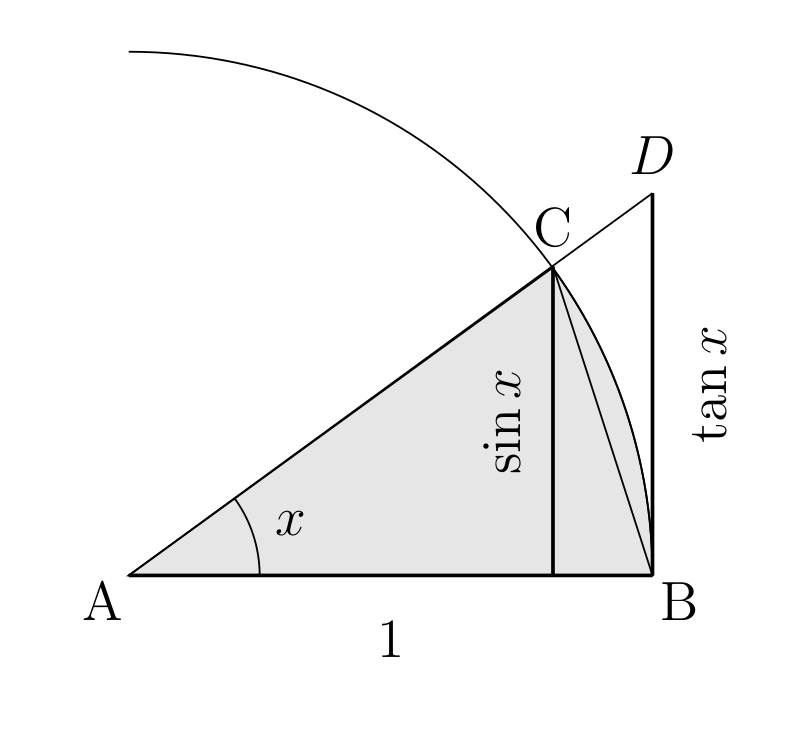
The area of \(\triangle ABC\) is less than that of sector \(ABC\) (which is \(x/2\), why? ¹ ), which is less than the area of \(\triangle ABD\):

Dividing by \(1/2 \sin x\) and taking reciprocals yields

and we can further take limits as \(x \to 0\) to obtain

The limit \(\displaystyle \lim_{x \to 0} \frac{\sin x}{x}\) is squeezed on both sides by 1 and cannot equal anything else but 1. Notice that we can replace \(x\) by any variable of our choosing, \(h\) for instance, and similarly obtain \(\displaystyle \lim_{h \to 0} \frac{\sin h}{h}=1\)

We are now ready to look into the derivative of \(\sin x\). By definition we have

Notice that a trigonometric identity for the sine of the sum of two angles was used to expand \(\sin(x+h)\). We recognize in the second term the limit we have looked at in the first part of the proof. However, it seems like we also need to evaluate \(\displaystyle \lim_{h \to 0} \frac{ \cos h - 1}{h}\). Fortunately, this limit can be deduced from the first using some trigometric identities, in particular \(\cos^2 h + \sin^2 h = 1\):

Putting everything together gives

Finally the differentiation formula \(\displaystyle \frac{d}{dx} \cos x = -\sin x\) can be obtained through a similar proof. We give here another proof based on some trigonometric identities and the Chain Rule which will be seen in Section 2.5:

The Chain Rule

Theorem: If \(g\) is differentiable at \(x\) and \(f\) is differentiable at \(g(x)\), then the composite function \(C\) defined by \(C(x) = f(g(x))\) is differentiable at \(x\) and

Proof:

Before we look into \(C'(x)\), we need some preliminary results. Recall \(\displaystyle g'(x) = \lim_{y \to x} \frac{g(y) - g(x)}{y-x}\), and since \(g'(x)\) is independent of \(y\), we can write

Define \(\epsilon\) as \(\displaystyle \epsilon = \frac{g(y) - g(x)}{y-x} - g'(x)\). From the previous equation we see that \(\epsilon\) approaches 0 as \(y\) approaches \(x\), that is \(\epsilon \to 0\) as \(y \to x\). Solving for \(g(y) - g(x)\) we obtain

Let \(Y = g(y)\) and \(X =g(x)\) and consider the expression

According to Equation (1), we can write \(f(Y) - f(X)\) as

where \(\psi \to 0\) as \(Y \to X\). Replacing \(Y\) and \(X\) respectively by \(g(y)\) and \(g(x)\), this gives

where \(\psi \to 0\) as \(g(y) \to g(x)\). Since \(g\) is differentiable at \(x\), it is also continuous at \(x\) and therefore \(\displaystyle \lim_{y \to x} g(y) = g(x)\), or \(g(y) \to g(x)\) as \(y \to x\). Therefore \(\psi \to 0\) as \(y \to x\).

If we replace \(y\) by \(x+h\), writing \(y \to x\) is the same as writing \(h \to 0\). Thus we have:

where \(\epsilon \to 0\) and \(\psi \to 0\) as \(h \to 0\).

We are now ready to compute \(C'(x)\) using Equations (2) and (3):

Since the function \(g\) is continuous at \(x=a\), then \(\lim_{x \to a} g(x) = g(a)\). Therefore